AI models keep getting smarter, but which one truly reasons under pressure? In this blog, we put o3, o4-mini, and Gemini 2.5 Pro through a series of intense challenges: physics puzzles, math problems, coding tasks, and real-world IQ tests. No hand-holding, no easy wins—just a raw test of thinking power. We’ll break down how each model performs in advanced reasoning across different domains. Whether you’re tracking the latest in AI or just want to know who comes out on top, this article has you covered.
What are o3 and o4-mini?
o3 and o4‑mini are OpenAI’s newest reasoning models, successors to o1 and o3‑mini that go beyond pattern matching by running a deeper, longer internal “chain of thought.” They can agentically invoke the full suite of ChatGPT tools and excel at STEM, coding, and logical deduction.
- o3: Flagship model with ~10× the compute of o1, capable of “thinking with images” for direct visual reasoning; ideal for in‑depth analytical tasks.
- o4‑mini: Compact, efficient counterpart optimized for speed and throughput; delivers strong math, coding, and vision performance at lower cost.
You can access both in ChatGPT and via the Responses API.
Key Features of o3 and o4-mini
Here are some of the key features of these advanced and powerful reasoning models:
- Agentic Behavior: They exhibit proactive problem-solving abilities, autonomously determining the best approach to complex tasks and executing multi-step solutions efficiently.
- Advanced Tool Integration: The models seamlessly utilize tools like web browsing, code execution, and image generation to enhance their responses and effectively tackle complex queries.
- Multimodal Reasoning: They can process and integrate visual information directly into their reasoning chain, which enables them to interpret and analyze images alongside textual data.
- Advanced Visual Reasoning (“Thinking with Images”): The models can interpret complex visual inputs, such as diagrams, whiteboard sketches, or even blurry or low-quality photos. They can even manipulate these images (zoom, crop, rotate, enhance) as part of their reasoning process to extract relevant information.
What is Gemini 2.5 Pro?
Gemini 2.5 Pro is Google DeepMind’s latest AI model, designed to offer improved performance, efficiency, and capabilities over its predecessors. It is part of the Gemini 2.5 series and represents the Pro-tier version, which strikes a balance between power and cost efficiency for developers and businesses.
Key Features of Gemini 2.5 Pro
Gemini 2.5 Pro introduces several notable enhancements:
- Multimodal Capabilities: The model supports various data types, including text, images, video, audio, and code repositories. It can thus handle a diverse range of inputs and outputs, making it a versatile tool across different domains.
- Advanced Reasoning System: At the core of Gemini 2.5 Pro is its sophisticated reasoning system, which enables the AI to analyze information before generating responses methodically. This deliberate approach allows for more accurate and contextually relevant outputs.
- Extended Context Window: It features an expanded context window of 1 million tokens. This allows it to process and understand larger volumes of information simultaneously.
- Enhanced Coding Performance: The model demonstrates significant improvements in coding tasks, offering developers more efficient and accurate code generation and assistance.
- Extended Knowledge Base: Compared to most other models, it is trained on more recent data, marking a cutoff in knowledge as of January 2025.
You can access Gemini 2.5 Pro via Google AI Studio or on the Gemini website (for Gemini Advanced subscribers).
o3 vs o4‑mini vs Gemini 2.5: Task Comparison Showdown
To see which model really shines across a spectrum of real‑world challenges, we put o3, o4‑mini, and Gemini 2.5 head‑to‑head on five very different tasks:
- Resonant Attenuation Reasoning: Computing the absorption coefficient, phase‑velocity ordering, and on‑resonance refractive index for a dispersive gaseous medium.
- Numerical Series Puzzle: Cracking a subtly growing sequence to pinpoint the missing term.
- LRU Cache Implementation: Designing a high‑performance, constant‑time Least Recently Used cache in code.
- Responsive Portfolio Webpage: Crafting a clean, mobile‑friendly personal site with semantic HTML and custom CSS.
- Multimodal Task Breakdown: Analyzing how each model would tackle an image‑based challenge.
Each test probes a different strength, in deep physics reasoning, pattern recognition, coding prowess, design fluency, and image‑context understanding; so you can see exactly where each model excels or falls short.
Task 1: Reasoning
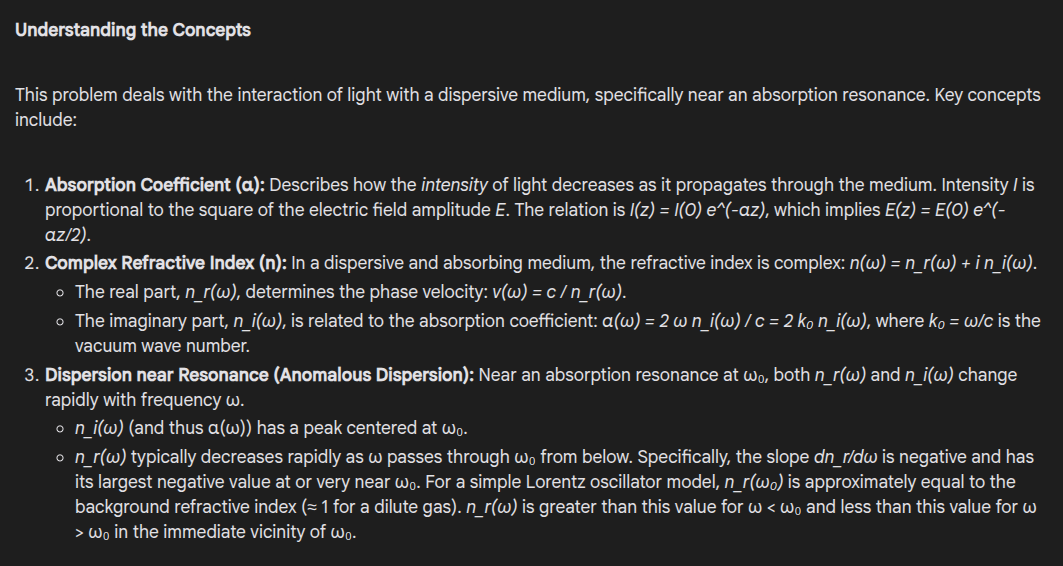
Input prompt: Dispersive Gaseous Medium. A dilute gaseous medium is found to exhibit a single optical resonance at frequency \\( \omega_0 = 2\pi \cdot 10^{15} \\) Hz. The electric field of a plane wave at frequency \\( \omega_0 \\) propagating through this medium is attenuated by a factor of two over a distance of 10 meters. The frequency width of the absorption resonance is \\( \Delta \omega \\). (a) What is the absorption coefficient \\( \alpha \\) at resonance? (b) Arrange in ascending order the propagation velocities at frequencies \\( \omega_0, \omega_0 + \Delta \omega / 10 \\), and \\( \omega_0 – \Delta \omega / 10 \\). Show your reasoning. (c) If there were no other resonances in the medium, what are the approximate numerical values of the index of refraction and the propagation velocity on resonance?
o3 Output:



o4-mini Output:



Gemini 2.5 Output:




Output Comparison
| Criteria | O3 | O4-mini | Gemini 2.5 |
| Absorption coefficient calculation | Correct with derivation; uses field decay equation and Beer–Lambert law | Correct and concise; uses κ and links to α clearly | Correct and detailed; uses logarithmic transformation and includes units |
| Ordering of phase velocities | Correct with mathematical clarity and physical explanation | Correct with crisp logical reasoning | Correct with strong conceptual background and intuitive reasoning |
| On-resonance index & velocity | Precise values with unit conversion and implications | Approximate but clear; assumes background index ≈ 1 | Qualitative explanation; slightly less quantitative |
| Clarity and depth of explanation | Deep but technical | Concise and student-friendly | Conceptually rich and well-structured; highly readable |
Final verdict:
All three models provide correct and coherent answers, but Gemini 2.5 stands out as the best overall performer. While O3 offers the most technical rigor, O4-mini excels in speed and clarity. Gemini 2.5 strikes the optimal balance between depth, conceptual clarity, and structured presentation. It not only delivers the correct results but also explains the underlying physics with intuitive reasoning, making it ideal for both understanding and verification.
Task 2: Numerical Reasoning
Input prompt: Select the number from among the given options that can replace the question mark (?) in the following series: 16, 33, 100, 401,?
o3 Output:

o4-mini Output:
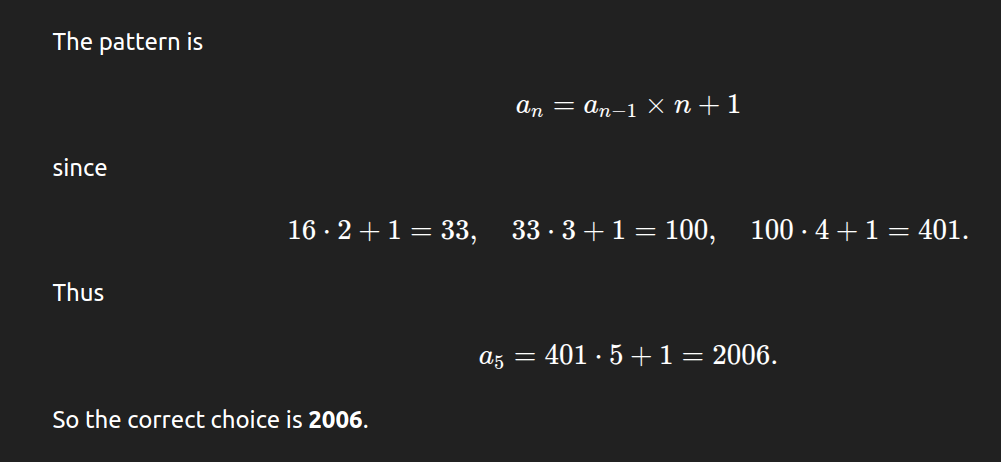
Gemini 2.5 Output:

Output Comparison
| Criteria | O3 | O4-mini | Gemini 2.5 |
| Correctness | Correct answer (2006) | Correct answer (2006) | Correct answer (2006) |
| Pattern Identification | Clear identification of increasing multiplier +1 | Identifies a recursive formula concisely | Walks step-by-step through the logic |
| Explanation Style | Slightly technical but neat | Clean and minimalistic | Most detailed and intuitive |
| Clarity for Students | Good for intermediate learners | Great for quick understanding | Excellent for all levels |
Final Verdict:
All three models correctly identify the pattern and arrive at the correct answer, 2006. While Gemini 2.5 provides a detailed, step-by-step explanation and O3 explains the logic clearly, O4-mini stands out for its elegance and mathematical precision. By expressing the sequence as a general formula, an=an−1×n+1a_n = a_{n-1} \times n + 1an=an−1×n+1, O4-mini captures the underlying pattern in the most concise and structured way. This makes it ideal for learners who appreciate clarity and compact reasoning. O4-mini delivers the best overall explanation.
Task 3: Coding task
Input prompt: Design and implement a data structure for Least Recently Used (LRU) cache. Implement the class `LRUCache` with the following methods:
– `get(key: int) -> int`: Return the value of the key if it exists, otherwise return -1.
– `put(key: int, value: int) -> None`: Update the value of the key if it exists, or insert the key-value pair if it doesn’t. When the cache reaches its capacity, it should invalidate the item that has been used least recently.
The cache should operate in O(1) time complexity for both operations.
o3 Code:
class Node:
"""Doubly‑linked‑list node holding a cache entry (key, value)."""
__slots__ = ("key", "value", "prev", "next")
def __init__(self, key: int, value: int):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity: int):
if capacity <= 0:
raise ValueError("Capacity must be positive")
self.cap = capacity
self.map: dict[int, Node] = {}
# Dummy head/tail simplify edge‑case handling
self.head = Node(0, 0) # Most‑recently‑used sentinel
self.tail = Node(0, 0) # Least‑recently‑used sentinel
self.head.next = self.tail
self.tail.prev = self.head
# ───────────────────────── Internal helpers ──────────────────────────
def _add_to_front(self, node: Node) -> None:
"""Insert node right after head (MRU position)."""
node.prev = self.head
node.next = self.head.next
self.head.next.prev = node
self.head.next = node
def _remove(self, node: Node) -> None:
"""Unlink node from list."""
node.prev.next = node.next
node.next.prev = node.prev
# ───────────────────────── Public API ────────────────────────────────
def get(self, key: int) -> int:
"""Return value if present; else ‑1. Marks entry as recently used."""
if key not in self.map:
return -1
node = self.map[key]
self._remove(node)
self._add_to_front(node)
return node.value
def put(self, key: int, value: int) -> None:
"""
Insert/update (key,value).
If capacity exceeded, evict the least‑recently‑used entry.
"""
if key in self.map: # Update existing
node = self.map[key]
node.value = value
self._remove(node)
self._add_to_front(node)
return
# Insert new key
node = Node(key, value)
self.map[key] = node
self._add_to_front(node)
# Evict if over capacity
if len(self.map) > self.cap:
lru = self.tail.prev # Real LRU node
self._remove(lru)
del self.map[lru.key]o4-mini Code:
class Node:
__slots__ = ('key', 'value', 'prev', 'next')
def __init__(self, key: int = None, value: int = None):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity: int):
self.capacity = capacity
self.cache = {} # key → Node
# Dummy head/tail
self.head = Node()
self.tail = Node()
self.head.next = self.tail
self.tail.prev = self.head
def _remove(self, node: Node):
"""Disconnect node from list."""
prev, nxt = node.prev, node.next
prev.next = nxt
nxt.prev = prev
def _add_to_front(self, node: Node):
"""Insert node right after head."""
node.next = self.head.next
node.prev = self.head
self.head.next.prev = node
self.head.next = node
def get(self, key: int) -> int:
if key not in self.cache:
return -1
node = self.cache[key]
# Move to front
self._remove(node)
self._add_to_front(node)
return node.value
def put(self, key: int, value: int) -> None:
if key in self.cache:
# Update existing node and move it to front
node = self.cache[key]
node.value = value
self._remove(node)
self._add_to_front(node)
else:
# Insert new node
new_node = Node(key, value)
self.cache[key] = new_node
self._add_to_front(new_node)
# Evict LRU if over capacity
if len(self.cache) > self.capacity:
# Tail.prev is LRU
lru = self.tail.prev
self._remove(lru)
del self.cache[lru.key]Gemini 2.5 Code:
import collections
class Node:
"""Node for the doubly linked list."""
def __init__(self, key, value):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity: int):
if capacity <= 0:
raise ValueError("Capacity must be a positive integer")
self.capacity = capacity
self.cache = {} # Stores key -> Node mapping
# Initialize sentinel nodes for the doubly linked list
self.head = Node(0, 0) # Dummy head
self.tail = Node(0, 0) # Dummy tail
self.head.next = self.tail
self.tail.prev = self.head
def _remove_node(self, node: Node):
"""Removes an existing node from the linked list."""
prev_node = node.prev
next_node = node.next
prev_node.next = next_node
next_node.prev = prev_node
# Optional: clear node pointers for garbage collection if needed
# node.prev = None
# node.next = None
def _add_to_front(self, node: Node):
"""Adds a node right after the head (most recently used)."""
node.prev = self.head
node.next = self.head.next
self.head.next.prev = node
self.head.next = node
def get(self, key: int) -> int:
"""
Return the value of the key if it exists, otherwise return -1.
Moves the accessed node to the front (most recently used).
"""
if key in self.cache:
node = self.cache[key]
# Move accessed node to the front
self._remove_node(node)
self._add_to_front(node)
return node.value
else:
return -1
def put(self, key: int, value: int) -> None:
"""
Update the value of the key if it exists, or insert the key-value pair.
Moves the updated/inserted node to the front.
Evicts the least recently used item if capacity is exceeded.
"""
if key in self.cache:
# Key exists, update value and move to front
node = self.cache[key]
node.value = value
self._remove_node(node)
self._add_to_front(node)
else:
# Key doesn't exist, insert new node
new_node = Node(key, value)
self.cache[key] = new_node
self._add_to_front(new_node)
# Check if capacity is exceeded
if len(self.cache) > self.capacity:
# Evict the least recently used item (node before tail)
lru_node = self.tail.prev
self._remove_node(lru_node)
# Remove from cache as well
del self.cache[lru_node.key]
# Example Usage:
try:
cache = LRUCache(2)
cache.put(1, 1) # cache is {1=1}
print(f"Cache after put(1, 1): {[(k, v.value) for k, v in cache.cache.items()]}")
cache.put(2, 2) # cache is {1=1, 2=2}
print(f"Cache after put(2, 2): {[(k, v.value) for k, v in cache.cache.items()]}")
print(f"get(1): {cache.get(1)}") # returns 1, cache is {2=2, 1=1} (1 is now MRU)
print(f"Cache after get(1): {[(k, v.value) for k, v in cache.cache.items()]}") # Order in dict might not reflect LRU order
cache.put(3, 3) # LRU key 2 was evicted, cache is {1=1, 3=3}
print(f"Cache after put(3, 3): {[(k, v.value) for k, v in cache.cache.items()]}")
print(f"get(2): {cache.get(2)}") # returns -1 (not found)
cache.put(4, 4) # LRU key 1 was evicted, cache is {3=3, 4=4}
print(f"Cache after put(4, 4): {[(k, v.value) for k, v in cache.cache.items()]}")
print(f"get(1): {cache.get(1)}") # returns -1 (not found)
print(f"get(3): {cache.get(3)}") # returns 3
print(f"Cache after get(3): {[(k, v.value) for k, v in cache.cache.items()]}")
print(f"get(4): {cache.get(4)}") # returns 4
print(f"Cache after get(4): {[(k, v.value) for k, v in cache.cache.items()]}")
except ValueError as e:
print(f"Error: {e}")Output Comparison
| Criteria | o3 | o4-mini | Gemini 2.5 |
| Readability | Excellent structure and comments | Very concise, less readable | Clear with helpful comments |
| Design & Modularity | Well-modularized, uses private methods | Minimalistic, lacks modular safety | Modular with helper methods and checks |
| Performance | Optimal with __slots__ & sentinels | Optimal and memory-efficient | Optimal, with optional GC suggestions |
| Safety & Robustness | Strong validation and clean error-handling | Lacks input checks (e.g., capacity ≤ 0) | Includes validation and safety guards |
Final Verdict
o3 offers the best balance of readability, safety, design, and performance, making it the most suitable for production and long-term use.
Task 4: Webpage Creation
Input prompt: Design a responsive personal portfolio webpage using HTML and CSS. The page should include the following sections:
1. Header: Display the user’s name and a brief tagline.
2. About Me: A short paragraph describing the user’s background and skills.
3. Projects: Showcase at least three projects with titles, descriptions, and links.
4. Contact: Provide contact information or a contact form.
Ensure the design is clean and mobile-friendly. Use semantic HTML elements and include basic CSS styling to enhance the visual appeal. Avoid using external CSS frameworks; write custom CSS for styling.
Implement the webpage in a single HTML file with embedded CSS.
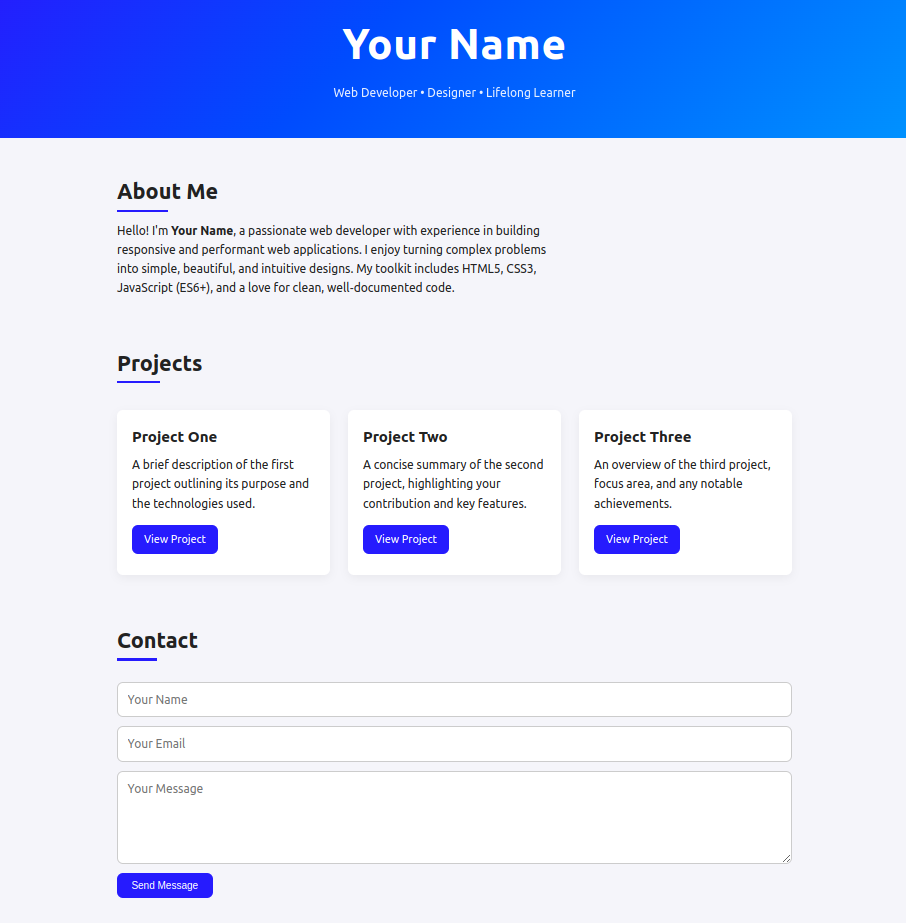
o3 Output:
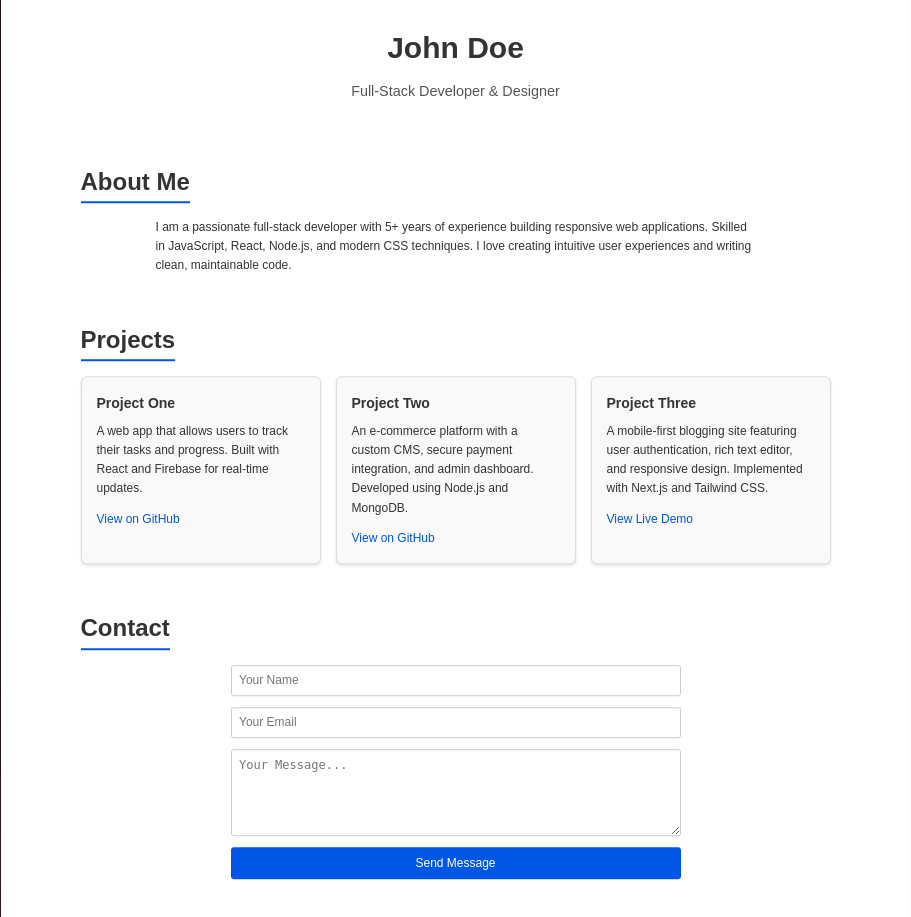
o4-mini Output:
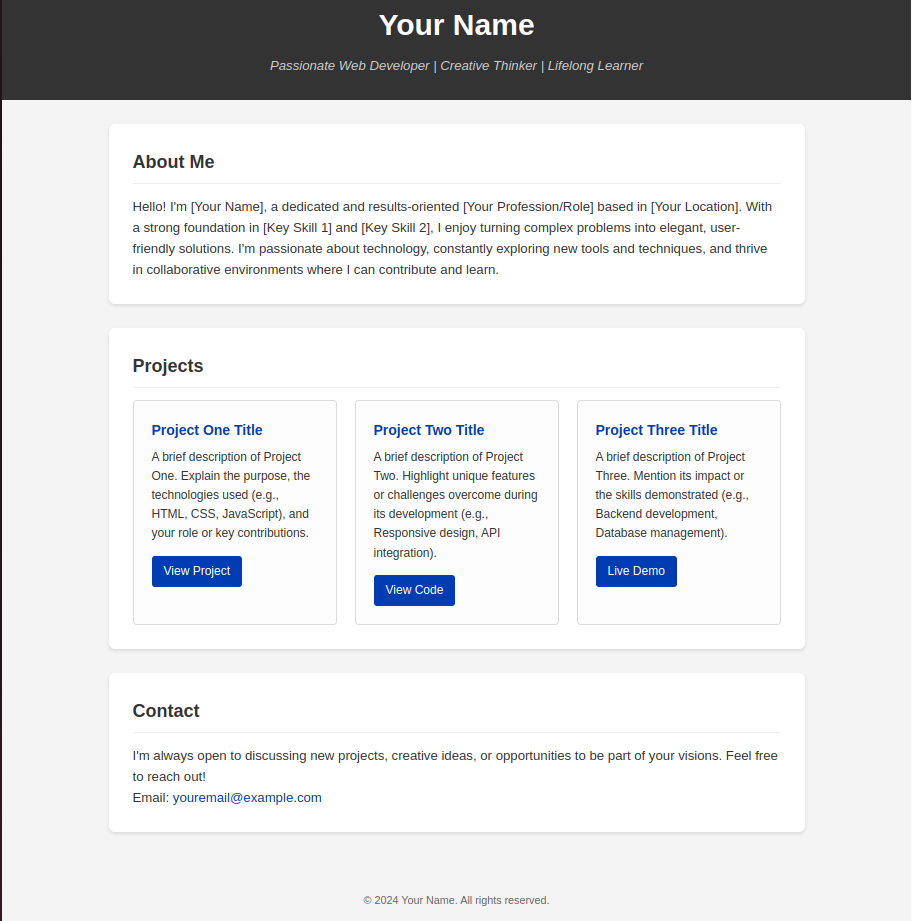
Gemini 2.5 Output:
Output Comparison
| Feature | o3 | o4-mini | Gemini 2.5 |
| Design Aesthetic | Modern, colorful with gradient header and consistent theme colors | Clean and minimalist with basic borders and box shadows | Clean layout with a minimalist design. Utilizes container width and padding for responsiveness. |
| Code Structure & Semantics | Excellent use of semantic HTML and comments; consistent BEM-style class naming | Clean semantic HTML, but less modular or commented | Well-structured with clear separation of HTML, CSS, and JS. Focus on semantic HTML with proper use of elements like <header>, <section>, and <footer>. |
| Responsiveness | Highly responsive with clamp(), auto-fit grids, and media queries | Basic responsiveness with flex-wrap and simple media queries | Good responsive with dynamic adjustments for various screen sizes, ensuring a proper user experience across devices. |
| Features Included | Full feature set: header, about, projects grid, contact (form & info), clean footer | Similar sections but lacks the polish in layout, interactivity, and styling finesse | Similar sections but lacks the polish in layout, interactivity, and styling finesse |
Final Verdict:
It features a more polished UI, improved responsiveness, modern CSS techniques (such as variables and clamp), and a professional overall presentation. It’s production-ready and showcases a deeper mastery of CSS.
Task 5: Image analysis
Input Image:
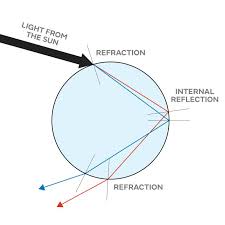
Input prompt: Explain the image to me in simple words, around 60 words
o3 Output:

o4-mini Output:

Gemini 2.5 Output:

Output Comparison
| Aspect | Output by o3 | Output by o4-mini | Output by Gemini 2.5 |
| Clarity | Clear, simple, and easy to understand. | Slightly more detailed, still clear. | Simple and easy to digest. |
| Explanation Depth | Balanced explanation with essential details. | More details on how colors bend. | Very basic explanation of the concept. |
| Tone/Style | Neutral, scientific, yet accessible. | Slightly conversational, still formal. | Very educational, designed for quick understanding. |
| Length | Compact, concise, covers all key points. | Longer, provides a bit more depth. | Very brief and to the point. |
Final verdict:
The o3 output provides the best balance of clarity, completeness, and simplicity, making it ideal for a general audience. It explains the process of a rainbow clearly, without overwhelming the reader with excessive details, while still covering essential aspects like refraction, internal reflection, and how multiple drops create the rainbow effect. Its concise style makes it easy to digest and understand, making it the most effective choice for explaining the phenomenon of a rainbow.
Overall Review
O3 is the best overall performer across all dimensions. It strikes the perfect balance between being scientifically accurate and easy to understand. While Gemini 2.5 is ideal for very basic understanding and O4-mini for more technical readers, O3 fits best for a general audience and educational purposes, offering a complete and engaging explanation without being overly technical or oversimplified.
Benchmark Comparison
To better understand the performance capabilities of cutting-edge AI models, let’s compare Gemini 2.5 Pro, o4-mini, and o3 across a range of standardized benchmarks. These benchmarks evaluate models across various competencies, ranging from advanced mathematics and physics to software engineering and complex reasoning.
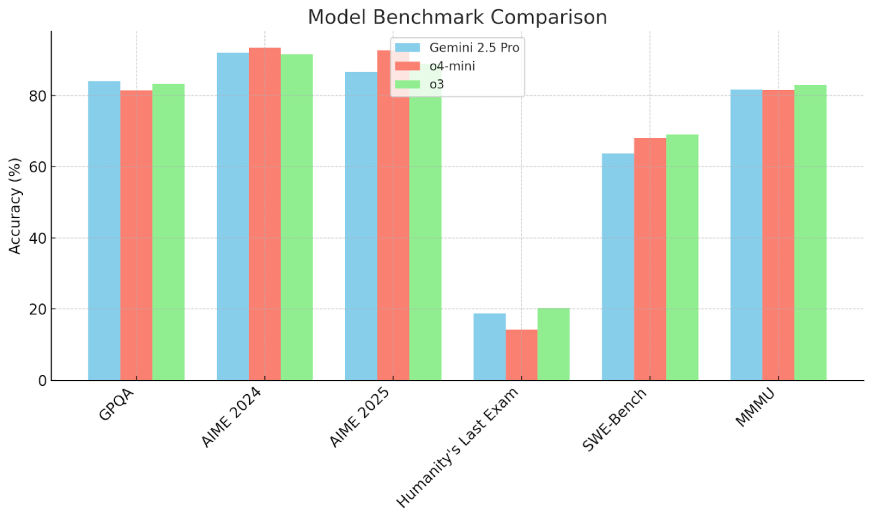
Key takeaways
- Mathematical reasoning: o4‑mini leads on AIME 2024 (93.4%) and AIME 2025 (92.7%), slightly outperforming o3 and Gemini 2.5 Pro.
- Physics knowledge: Gemini 2.5 Pro scores highest on GPQA (84%), suggesting strong domain expertise in graduate‑level physics.
- Complex reasoning challenge: All models struggle on Humanity’s Last Exam (<21%), with o3 at 20.3% as the top performer.
- Software engineering: o3 achieves 69.1% on SWE-Bench, edging out o4‑mini (68.1%) and Gemini 2.5 Pro (63.8%).
- Multimodal tasks: o3 also tops MMMU (82.9%), though differences are marginal.
Interpretation & implications
These results highlight each model’s strengths: o4‑mini excels in structured math benchmarks, Gemini 2.5 Pro shines in specialized physics, and o3 demonstrates balanced capability in coding and multimodal understanding. The low scores on “Humanity’s Last Exam” reveal room for improvement in abstract reasoning tasks.
Conclusion
Ultimately, all three models, o3, o4‑mini, and Gemini 2.5 Pro, represent the cutting edge of AI reasoning, and each has different strengths. o3 stands out for its balanced prowess in software engineering, deep analytical tasks, and multimodal understanding, thanks to its image‑driven chain of thought and robust performance across benchmarks. o4‑mini, with its optimized design and lower latency, excels in structured mathematics and logic challenges, making it ideal for high‑throughput coding and quantitative analysis.
The Gemini 2.5 Pro’s massive context window and native support for text, images, audio, and video give it a clear advantage in graduate-level physics and large-scale, multimodal workflows. Choosing between them comes down to your specific needs (for example, analytical depth with o3, rapid mathematical precision with o4‑mini, or extensive multimodal reasoning at scale with Gemini 2.5 Pro), but in every case, these models are redefining what AI can accomplish.
Frequently Asked Questions
Gemini 2.5 pro supports a context window of up to 2 million tokens, significantly larger than that of O models.
O3 and O4-mini generally outperform Gemini 2.5 in advanced coding and software engineering tasks. However, Gemini 2.5 is preferred for coding projects requiring large context windows or multimodal inputs.
Gemini 2.5 Pro is roughly 4.4 times more cost-effective than O3 for both input and output tokens. This makes Gemini 2.5 a strong choice for large-scale or budget-conscious applications.
Gemini 2.5 Pro: Up to 2 million tokens
O3 and O4-mini: Typically support up to 200,000 tokens
Gemini’s massive context window allows it to handle much larger documents or datasets in one go.
Yes, but with key distinctions:
O3 and O4-mini include vision capabilities (image input).
Gemini 2.5 Pro is natively multimodal, processing text, images, audio, and video, making it more versatile for cross-modal tasks.
Login to continue reading and enjoy expert-curated content.